데이터 관리하는데 있어 콜렉션들이 가물가물해져서 정리
- 데이터 구조란 - 데이터를 메모리에 저장할 떄 데이터의 순서나 위치 관계 등을 정하는 것.
- 데이터 구조를 고민해서 메모리 이용 효율을 높여야한다.
- 목적에 맞게 구조화해서 메모리의 이용 효율을 높이자.
- 확장 - 원형 리스트(순환리스트), 양방향 리스트
리스트
데이터를 일직선으로 나열한 형태를 가지고 있다.
데이터 추가나 삭제는 쉽지만, 데이터에 접근하려면 시간이 많이 걸린다.
- 데이터가 메모리상의 연속된 우치에 저장되지 않아도 되며, 일반적으로 떨어져 흩어져 저장된다. 그러므로 포인터를 처음부터 순서대로 따라가야만 원하는 데이터 접근 가능.
- 순차접근구조
- 데이터 추가시 포인터로 연결 끊고 추가 후 새로 다시 걸어줘야한다.
- 삭제도 마찬가지로 포인터 연결 끊고 삭제 후 다시 연결
- 앞에서 부터 차례대로 진행하므로 선형탐색이라고 불린다.
- 데이터 검색 시간은 O(n)의 시간이 걸린다. 반면 데이터 추가는 두개의 포인터만 바꾸면 되므로 개수(n) 상관없이 O(1)상수 시간이 된다. 삭제도 마찬가지로 O(1)상수시간\
배열
데이터를 1열로 나열한 것, 리스트와는 대조적으로 접근하기는 쉽지만, 추가삭제에 시간이 걸린다.
데이터는 연속된 메모리 영역에 순서대로 저장됩니다.
연속된 영역에 저장되어 있어 첨자를 사용해 메모리의 주소를 계산할 수 있따. “임의접근 가능
- 배열의 저장된 데이터 수가 n이라고 할 떄, 임의 접근할 수 있으므로 상수 O(1)의 시간으로 접근할 수 있지만, 추가 삭제할 떄는 뒤에 있는 모든 데이터를 하나씩 옮겨야 하므로 O(n)의 시간이 걸립니다.
스택
데이터를 1열로 나열하지만, 서류를 쌓아 놓은 경우처럼 새롭게 추가한 데이터에만 접근 가능.
아래에서 부터 쌓이면서 위로 올라간다.
-
나중에 넣은 것을 먼저 꺼내는 후입선출 구조 - Last In First Out(LIFO)
-
스택은 단방향으로만 조작할 수 있다는 제약이 있어 불편하다고 생각 할 수 있지만, 항상 최신 데이터만 접급할 수 있도록 하는 구조에서는 편리하게 사용 가능.
깊이 우선 탐색에선느 탐색 후보 중에서 항상 최신의 것을 선택해야 하므로 후보관리에 스택을 활용한다.
큐
데이터를 1열로 나열한 구조이며,스택과 비슷하지만, 큐는 추가하는 측과 삭제하는 측이 반대이다.
큐는 대기행렬 이라고도 불린다. 행렬에서는 새롭게 온 사람이 가장 뒤에 서며, 가장 앞에 있는 사람이 순서대로 처리된다.
-
먼저 넣은 것을 먼저 꺼내는 선입선출 구조 - First In First Out(FIFO)
-
오래된 데이터부터 순서대로 처리해야 하는 것은 매우 자연스러운 방식이라 큐는 폭넓게 활용 되었다. 너비 우선 탬색에서는 탐색 후보 중에서 항상 가장 오래도니겅르 선택하므로 후보 관리에 큐를 활용한다.
해시테이블
해시 함수와 함께 데이터 검색을 효울적으로 하기 위해 사용되는 구조이다.
- 해시 테이블은 키(Key)와 값(Value)이 한 쌍을 이루는 데이터를 저장합니다.
하지만 배열의 선형탐색처럼 key값을 검색한다면 데이터양에 비례해서 계산시간이 느러난다.
이 문제를 해결해 주는것이 해시테이블이다.
-
해시 테이블은 데이터 추가시 해시 함수를 이용해서 키에 해당하는 해시값을 계산, 만약 4928이라는 값이 나온다면 배열의 상자수로 나누어 나머지를 구합니다. 구한수와 같은 배열의 숫자 상자에 키값의 데이터를 저장.
-
만약 해시 값이 동일해서 겹치는걸 충돌 이라고 하는데, 이런 경우에는 리스트 구조로 기존 데이터와 연결
-
검색 방법은 해당 키 데이터가 배열의 몇번 상자에 저장돼 있는지 알기 위해서 해당 키의 해시값을 구하고 배열 상자 수로 나머지 연산을 합니다.
-
but 해당 배열 상자에 몇번쨰인지 해시 값으로 찾았지만 중첩된 데이터가 많은경우, 해당 저장은 리스트로 되어 있으므로, 선형탐색을 실시한다.
해시 테이블은 해시 함수를 이용해서 배열 내의 특정 데이터에 빠르게 접근 할 수 있다.
해시값이 충돌할 떄는 리스트를 이용하므로 저장할 데이터 수가 정해져 있지 않더라도 유연하게 대응 가능.
해시테이블 데이터 크기가 너무 작으면 충돌이 많아지고,
성형탁색의 빈도가 높아진다. 반대로 너무 크면 데이터가 없는 상자가 많아져 메모리 낭비를 하게 된다.
따라서 적절하게 크기를 설정하는것이 중요!!
힙
힙은 그래프의 트리 구조 중 하나로, ‘우선순위 큐(prioiry queue)‘를 구현할 떄 사용된다.
우선순위 큐는 데이터 구조의 하나로서 데이터를 자유롭게 추가할 수 있다, 반면 데이터 추출할 떄는 최솟값부터 순서대로 선택된다.
추가는 자유롭게 하고 추출은 작은 값부터 꺼내는 것이 우선순위 큐 이다.
힙을 표현하는 트리 구조에서는 각 정점을 노트라고 부른다. 힙에서는 각 노드에 데이터가 저장됩니다.
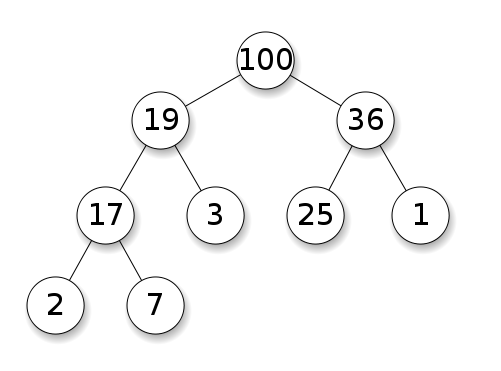
- 힙의 노드들은 최대 두 개의 자식 노드를 가집니다. 또한, 트리의 모양은 데이터의 개수에 의해 정해진다. 노드는 위에서부터 채워지며, 같은 층에서는 왼쪽부터 채워진다.
- 힙에서는 데이터 저장 위치를 정하기 위해 자식 노드의 숫자는 반드시 부모의 숫자보다 커야한다는 규칙이 있다. 그러므로 가장 위(뿌리)에 가장 작은 숫자가 들어있다.
- 만약 숫자가 더 작은 노드가 추가된다면 부모와 교체 하는 식으로 자리 교체를 한다.(반복)
- 힙에서 숫자를 꺼낼 떄는 가장 위에 있는 숫자가 추출된다. (가장 위 숫자가 최솟값을 지니므로) -> 가장 위에 숫자가 없어졌으므로 힙의 구조를 다시 정리한다. -> 가장 후미에 있는 숫자가 위로 올라가고 -> 부모와 자식 숫자비교를 통해 교환(반복) -> 숫자 추출 처리 완료
힙은 항상 가장 위에 최솟값이 있으므로 데이터 수 상관없이 O(1)상수 시간에 최솟값을 추출 할 수 있다.
추출한 후에 힙을 재구축할 떄에는 가장 후미에 있는 데이터가 위로 온 후
비교하며 진행하므로 계산 시간은 트리의 높이와 비례데이터 수를 n이라고
하면 힙 형성 조건에 따라 트리의 높이는 log2n 이므로 재구축의 시간은 O(log n)이다.
활용 예로 다익스트라 알고리즘에서는 후보가 되는 노드 중에서 최솟값을 매 단계에서 선택하는데,
이떄 노드를 관리하기 위해 힙을 사용하는 경우가 있습니다.
정렬 알고리즘 중에 worst인경우 시간복잡도 가장 효율적
이진탐색트리
데이터 구조의 하나로, 그래프의 트리 구조를 사용합니다.
이진 탐색의 개념을 트리구조로 표현한것.
각 노드에 데이터가 저장 된다
-
두 가지 성실을 지닌다.
- 모든 노드는 왼쪽 가지에 포함되는(자식) 어떤 숫자보다도 큰 숫자가 된다.
- 모든 노드는 그 노드의 오른쪽 가지(자식)에 포함되는 어떤 숫자보다 작은 숫자가 된다.
-
이 두 성질에 따라 다음 조건이 성립된다.
- 이진 탐색 트리의 최소 노드는 최상단에 있는 노드로 부터 왼쪽 가지만 계속 따라가면 나오는 가장 끝에 있는 노드이다.
- 반대로 최대 노드는 최상단 노드로 부터 오른쪽 가지만 따라가면 나오는 가장 끝에 있는 노드이다.
-
이진탐색트리 추가하는 경우
- 최상단 노드부터 탐색해 간다.
- 값 비교해서 작으면 왼쪽, 크면 오른쪽으로 진행(반복)
-
이진탐색트리 삭제하는 경우
- 자식 노드가 없는 경우 대상 노드를 삭제만 하면 긑
- 자식 노드가 1개인 경우 대상 노드를 삭제하고 삭제한 노드의 우치로 자식노드를 이동시키면 된다.
- 자식 노드가 2개인 경우 대상 노드를 삭제하고 왼쪽 가지에서 최대 노드를 찾는다 -> 그 노드를 삭제한 노드 위치로 이동시킨다. 이동 대상 노드도 자식 노드 지닌 경우 같은 처리를 재귀적으로 반복
-
이진탐색트리 탐색 방법
- 최상단 노드부터 탐색을 시작. 찾으려는 값과 비교하며 작으면 왼쪽, 크면 오른쪽으로 진행한다.
비교 시 트리의 높이 만큼 비교 하므로 노드가 n개이고 균형잡힌 트리라면
최대 log2n회의 비교로 이동 따라서 계산시간은 O(log n)이다.
단 최악의 경우 - 트리가 한쪽으로 치우쳐 직선에 가까운 모양이면 O(n)이 될 수 있따.
확장해 트리 균형을 위해 "자가 균형 이진 탐색트리"존재,
또한 자식 노드 수 제한을 두지 않고 트리의 균형을 도모한 "B 트리"도 존재한다.